Singular value decomposition
I don't know how I have not learned this until today because it is very important.
Given any real square matrix $A$, we can write
$$ A=U \Sigma V $$where $U$ and $V$ are orthogonal matrices and $\Sigma$ is a diagonal matrix with non negative entries.
The meaning of this is easy: any linear transformation of a vector space can be obtained by a rigid transformation (rotation or reflection), followed by a scale change in the main axis direction (and different scales could be applied in every axis) and finally followed by another rigid transformation.
It is related to the polar decomposition.
Visualization: see this web.
Non square matrices
This also works for non square matrices. Consider that $A$ is the $n\times m$ matrix of a transformation $T:\mathbb{R}^n \to \mathbb{R}^m$. Then again $A=U \Sigma V$ where $U$ and $V$ are square orthogonal matrices of dimension $m$ and $n$ respectively. But now, $\Sigma$ is a non square diagonal matrix with non-negative entries.
The $m$ columns of $U$ represent a orthonormal basis of $\mathbb{R}^m$, $B_U$. And the $n$ columns of $V$ are a orthonormal basis of $\mathbb{R}^n$, $B_V$. The transformation $T$ can be understood like the one which sends the $i$th element of $B_V$ to the $i$th element of $B_U$ multiplied by the (non-negative) diagonal element $\sigma_{ii}$ of $\Sigma$. This happens for every linear transformation!
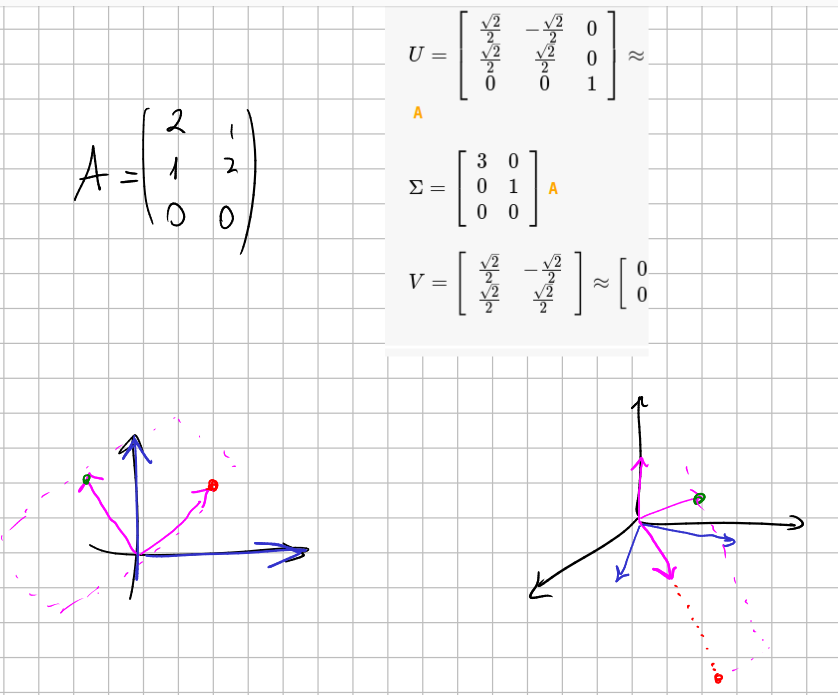
It is related to matrix diagonalization. Indeed they are equal when the matrix is symmetric positive-demidefinite.
________________________________________
________________________________________
________________________________________
Author of the notes: Antonio J. Pan-Collantes
INDEX: